For over 20 years, the four percent rule has served as an invaluable benchmark for gauging whether or not a retiree is overspending from their portfolio. However, the four percent rule is a theoretical model, not a withdrawal strategy. Retirees don’t automatically increase their monthly stipend at the beginning of each year by the prior year CPI increase.
Retirees are often told that they need to monitor their portfolio periodically and adjust their withdrawal when necessary. Unfortunately, this task is easier said than done. There is a great need for a tool to address this challenge.
Retirement researchers have proposed various metrics to determine when the long-term sustainability of a retiree’s portfolio is at risk and what actions to take when this occurs to extend portfolio lifetime. Unfortunately, these techniques are too cumbersome or not effective enough to implement as a withdrawal strategy. That’s why I developed the six percent method.
The Six Percent Method
Here’s how it works. In the initial year of retirement, the retiree withdraws six percent of their portfolio to pay their living expenses including income taxes and investment fees. Each year thereafter the retiree may increase their annual withdrawal for inflation only if the resulting annual withdrawal is less than six percent of their portfolio at the beginning of the year. For example, let’s assume that at the beginning of year 10 of retirement, Mary’s portfolio is $800,000. In year nine, Mary withdrew $50,000 from her portfolio to pay living expenses and the CPI increased by two percent. If Mary took an inflation increase at the beginning of year 10, her annual withdrawal for year 10 would be $51,000. Since $51,000 exceeds six percent of $800,000, Mary should not take an inflation increase for the year. Her annual withdrawal for year 10 should be $50,000, the same as she withdrew in year nine.
If Mary’s retirement portfolio had been $900,000, then she would have been safe to take an inflation increase at the beginning of year 10 because $51,000 is less than six percent of $900,000.
Probability Of Success Remains About The Same
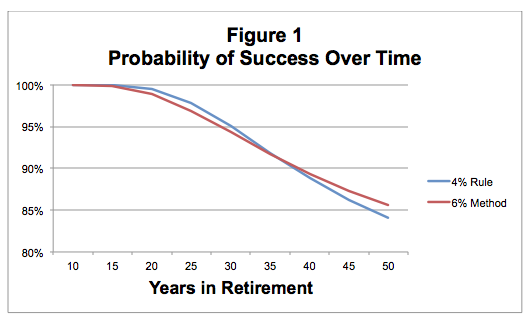
Figure 1 shows a comparison of the probability of success under the four percent rule and the six percent method. Probabilities are based on a model portfolio of 50 percent stocks and 50 percent bonds. As you can see, the four percent rule has a slightly higher success probability in the early years, but the six percent method wins in the later years of retirement. Overall, the probabilities are very close. Note that the difference in the probability of success between the two approaches is less than one percent during each of the first 40 years of retirement.
Purchasing Power
The four percent rule provides that the purchasing power of withdrawals will never decline. Under the six percent method, purchasing power may decline over time.
Table 1 illustrates the probability of purchasing power decline under the six percent method. On the upside, there’s a better than 10 percent chance you will never need to skip an inflation increase, and your purchasing power will remain unchanged (the top decile). On the downside, there’s a 10 percent probability that purchasing power in year 30 of retirement will be 42 percent or less of your original purchasing power (the bottom decile).








